Endboss Heap-Sort

Als programmiertechnische Funktion sind für den Heap-Sort Sortieralgorithmus bedingte Verzweigungen für if-then Konstrukte und Schleifen notwendig. Ausserdem muss über eine indirekte Adressierung auf die Register zugegriffen werden.
Der Code für den HP-16C. Die Wortbreite im Integer-Modus ist auf 24 gestellt, um mehr Speicherzellen zu erhalten. In R0 muss die Größe der zu sortierenden Liste stehen, ab R1 die Listenelemente :
001 43.22. A Lbl A # swap 002 45 .E RCL .E 003 42 22 x<>I 004 42 21 x<>(i) 005 45 .D RCL .D 006 42 22 x<>I 007 42 21 x<>(i) 008 34 x<>y 009 42 21 x<>(i) 010 42 22 x<>I 011 33 R↓ 012 42 21 x<>(i) 013 43 21 RTN 014 43.22. B Lbl B # heapify 015 45 .F RCL .F 016 44 .E STO .E 017 43.22. D Lbl D 018 2 2 019 10 ./. 020 44 .D STO .D 021 42 22 x<>I 022 45 31 RCL(i) 023 45 .E RCL .E 024 42 22 x<>I 025 33 R↓ 026 45 31 RCL(i) 027 43 1 x<=y? 028 21 A GSB A 029 1 1 030 45 .E RCL .E 031 1 1 032 30 - 033 44 .E STO .E 034 43 0 x!=y? 035 22 D GTO D 036 43 21 RTN 037 43.22. C Lbl C # main 038 45 0 RCL 0 039 44 .F STO .F 040 43.22. E Lbl E 041 21 B GSB B 042 45 .F RCL .F 043 44 .E STO .E 044 1 1 045 44 .D STO .D 046 21 A GSB A 047 45 .F RCL .F 048 1 1 049 30 - 050 44 .F STO .F 051 2 2 052 43 0 x!=y? 053 22 E GTO E 054 43 21 RTN R 0 # heap size R 1 - # elements R .F # size heapify R .E # index leave R .D # index node
Die Implementation für den HP-16C als auch für den TI-58C verwenden von der Programmstruktur vergleichbare Funktionen.
- Hauptprogramm
Die Listenelemente werden in einer Baumstruktur angeordnet. Zwei Elemente (leaf) sind einem Element (node) zugeordnet. Der zugehörige Index beginnt bei eins, für ein node-Element berechnet er sich :
i[node] = int( i[leaf] / 2)
Der TI-58C verwendet bei der indirekten Adressierung implizit nur den Integer-Teil einer gespeicherten Zahl. 2,7 zeigt als Pointer also auf das Register R02. Der HP-16C berechnet bei Division im Integer Modus den Vorkomma-Teil, der Rest einer Integer-Division wird mit der Modulo Funktion RMD (remainder) ausgegeben.
Nach Aufrufen der Funktion heapify befindet sich das größte (kleinste) Element dieser Liste auf Index-Position 1. Dieses Element wird mit dem auf der letzten Position getauscht, die Länge der Liste um eins verringert.
- Unterprogramm Heapify
Jeweils zwei Elemente (leaf, node) werden verglichen, und ggf. getauscht (Funktion swap), so dass immer die größere Zahl auf der übergeordneten node Position steht. Müssen bei einem Durchlauf, dem Testen aller Elemente, keine Elemente mehr getauscht werden, ist das größte Element auf Position 1. FALSCH IMPLEMENTIERT!
- Unterprogramm Swap
Das Tauschen von zwei Registerwerten wird über indirekte Adressierung und Zwischenspeicherung im x, y bzw. Display-Register durchgeführt.

Der Code für den TI-58C, die Partitionierung muss 50 Register ermöglichen :
000 76 LBL # swap 001 11 A 002 63 EXC IND 003 48 48 004 63 EXC IND 005 47 47 006 63 EXC IND 007 48 48 008 92 RTN 009 76 LBL # heapify 010 12 B 011 43 RCL 012 B 49 013 42 STO 014 48 48 015 76 LBL 016 17 B' 017 42 STO 018 47 47 019 02 2 020 22 INV 021 49 PRD 022 47 47 023 73 RCL IND 024 47 47 025 32 X<>T 026 73 RCL IND 027 48 48 028 77 X>=T? 029 19 D' 030 76 LBL 031 10 E' 032 01 1 033 22 INV 034 44 SUM 035 48 48 036 02 2 037 32 X<>T 038 43 RCL 039 48 48 040 77 X>=T? 041 17 B' 042 92 RTN 043 76 LBL 044 19 D' 045 11 A 046 61 GTO 047 10 E' 048 76 LBL # main 049 13 C 050 43 RCL 051 00 00 052 42 STO 053 49 49 054 76 LBL 055 18 C' 056 12 B 057 43 RCL 058 49 49 059 42 STO 060 48 48 061 01 1 062 42 STO 063 47 47 064 11 A 065 01 1 066 22 INV 067 44 SUM 068 49 49 069 02 2 070 32 X<>T 071 43 RCL 072 49 49 073 77 X>=T? 074 18 C' 075 92 RTN R00 # heap size R01-46 # elements R49 # size heapify R48 # index leave R47 # index node
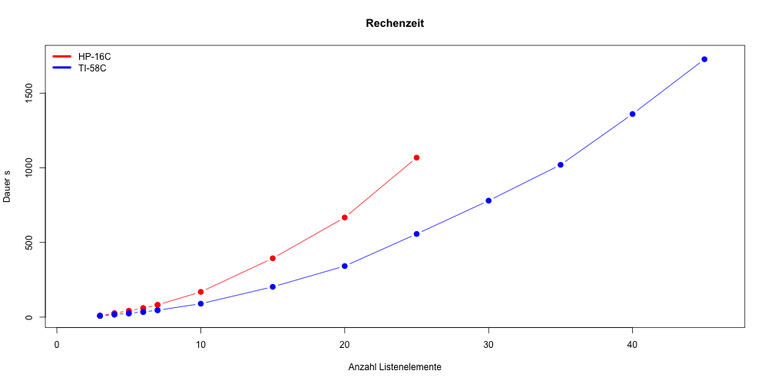
Eine praktische Laufzeitanalyse zeigt, die Implementation ist kein Heap-Sort, sondern ein dilletantischer Bubble-Sort.