Code Schnipsel
Inharmonische Saitenspektren

In Inharmonic strings and the hyperpiano wird beschrieben, wie mit verschieden starken Segmenten auf einer schwingenden Saite gezielt ein inharmonisches Klangspektrum erzeugt werden kann. Dies bedeutet, dass die Frequenzen der Teiltöne nicht zwangsläufig ganzzahlige Vielfache der Grundfrequenz sein müssen. Die numerische Lösung erfordert Matrixoperationen und ein Näherungsverfahren zur Nullstellensuche. Diese Herausforderung ist mit programmierbaren Taschenrechnern lösbar.
Im HP-42S werden die verschieden starken Saitensegmente jeweils durch eine 2x2 Matrix repräsentiert, das Produkt der Matrizen gibt in einer Zelle als Nullstelle die Frequenzen der Teiltöne. Der eingebaute Solver erledigt die Nullstellensuche mit entsprechend eingegrenztem Suchbereich zuverlässig.
01 LBL "INHX" # Main-Loop für den Solver 02 MVAR "W" 03 RCL "Vµ1" 04 STO "µ" 05 RCL "VL1" 06 STO "L" 07 XEQ "MTRX" 08 STO "MZ" 09 RCL "Vµ2" 10 STO "µ" 11 RCL "VL2" 12 STO "L" 13 XEQ "MTRX" 14 STOx "MZ" 15 INDEX "MZ" 16 1 17 ENTER 18 2 19 STOIJ 20 RCLEL 21 RTN 22 .END. 01 LBL "MTRX" # Berechnung der Matrix für ein Saitensegment 02 2 03 ENTER 04 2 05 NEWMAT 06 STO "MT" 07 INDEX "MT" 08 RCL "µ" 09 RCL "T" 10 / 11 SQRT 12 RCL "W" 13 x 14 STO "K" 15 RCL "L" 16 x 17 STO "KL" 18 COS 19 STOEL 20 1 21 ENTER 22 2 23 STOIJ 24 RCL "KL" 25 SIN 26 RCL "K" 27 / 28 +- 29 STOEL 30 2 31 ENTER 32 1 33 STOIJ 34 RCL "KL" 35 SIN 36 RCL "K" 37 x 38 STOEL 39 2 40 ENTER 41 2 42 STOIJ 43 RCL "KL" 44 COS 45 STOEL 46 RCL "MT" 47 RTN 48 .END. µ Dichte des Segments Vµ1 Dichte 1 Vµ2 Dichte 2 T Saitenspannung L Länge des Segments VL1 Länge 1 VL2 Länge 2
Mit unterschiedlichen Längen der dichten und leichten Saitensegmente ergibt sich eine Verschiebung der Frequenzen der Teiltöne, die Saite klingt Inharmonisch, "metallischer".

Die Berechnung basiert auf zwei Saitensegmenten. Weitere Versuche müssen zeigen, inwieweit mehr Segmente die Verschiebung der Teiltöne beeinflussen. Das nächste Ziel ist, für ein beliebig vorgegebenes Spektrum (für Konsonanzoptimierung in einer beliebigen Skala) mittels eines Gradientenabstiegverfahrens die Position und Länge von Saitensegmenten zu berechnen / optimieren.
Aus Performance-Gründen wird die Umsetzung in einer modernen PC-Umgebung stattfinden. ;-)
Faktoren für Frequenzen der Teiltöne
Der Dichteunterschied für verschiedene Saitensegmente und die Längen der Teilstücke scheinen offensichtliche Faktoren für die Verteilung der Frequenzen der Teiltöne zu sein. [Die Saitenspannung ändert zwar die Tonhöhe, aber nicht die Frequenzverteilung der Teiltöne] (Dies ist noch zu klären).
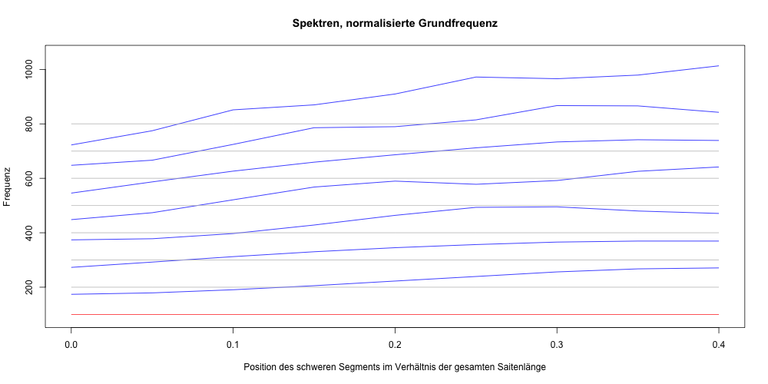
Bei drei verwendeten Segmenten zeigt sich, dass die Position des mittleren, schweren Teilstücks Einfluss auf die Teiltonfrequenzen hat. (Länge Mittelteil (0,2) und Gesamtlänge (1,0) bleiben konstant)
Je weiter ein schweres Mittelstück zur Saitenmitte wandert, umso weiter wandern die Teiltöne unterschiedlich auseinander. (x ≈ L1)
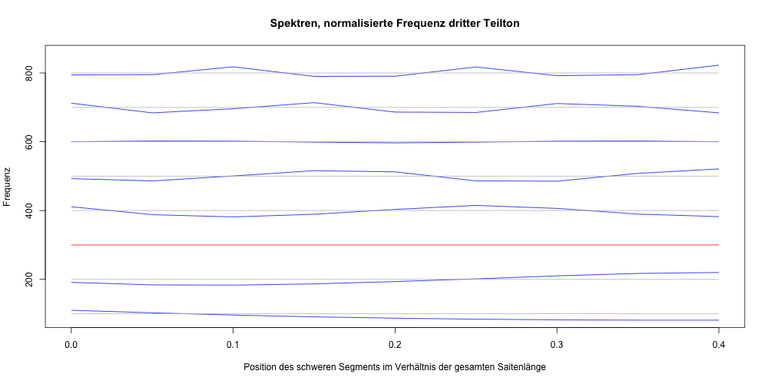
Die Frequenzen des dritten Teiltons gleich gestimmt:
Anzahl der Segmente
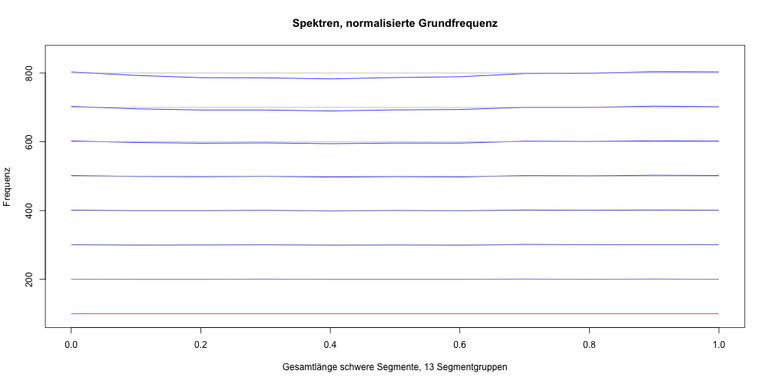
Ein gleichbleibendes Verhältnis der Gesamtlänge von schweren zu leichten Saitensegmenten erzeugt bei unterschiedlicher Verteilung verschiedene Spektren. Eine Segmentgruppe besteht hier aus zwei gleich langen, verschieden schweren Teilstücken. Die Anzahl der Segmentgruppen wird variiert.

Bei gleichbleibender Anzahl der Segmentgruppen mit verändertem Verhältnis von schweren und leichten Teilstücken zeigt sich keine nennenswerte Änderung in der Verteilung der Teiltonfrequenzen. Vorausgesetzt es werden Teiltöne betrachtet, deren Wellenlänge größer als die Länge einer Gruppe schweres / leichtes Saitensegment ist. Hier 13 Segmentgruppen, Darstellung bis zum 8. Teilton.
Der Soundtrack zum Projekt. ;-)
Heap-Sort

TI-58C Code für Heap-Sort :
000 76 Lbl 001 92 RTN 002 92 RTN 003 76 Lbl # swap bedingt 004 11 A 005 22 INV 006 77 x≥t? 007 92 RTN 008 67 x=t? 009 92 RTN 010 76 Lbl # swap 011 16 A' 012 63 Exc Ind 013 24 24 014 63 Exc Ind 015 25 25 016 63 Exc Ind 017 24 24 018 86 St flg 019 01 1 020 92 RTN 021 76 Lbl # node + leaf pointer setzen 022 23 lnx 023 53 ( 024 43 RCL 025 24 24 026 65 x 027 02 2 028 54 ) 029 42 STO 030 26 26 031 53 ( 032 24 CE 033 85 + 034 01 1 035 54 ) 036 42 STO 037 27 27 038 92 RTN 039 76 Lbl # heapify 040 33 x² 041 71 SBR 042 23 lnx 043 43 RCL 044 27 27 045 32 x<>t 046 43 RCL 047 28 28 048 77 x≥t? 049 19 D' 050 43 RCL 051 28 28 052 32 x<>t 053 43 RCL 054 26 26 055 67 x=t? 056 17 B' 057 92 RTN 058 76 Lbl # swap left leaf 059 17 B' 060 43 RCL 061 26 26 062 42 STO 063 25 25 064 73 RCL Ind 065 24 24 066 32 x<>t 067 73 RCL Ind 068 25 25 069 71 SBR 070 11 A 071 92 RTN 072 76 Lbl # swap double leaf 073 19 D' 074 73 RCL Ind 075 27 27 076 32 x<>t 077 73 RCL Ind 078 26 26 079 77 x≥t? 080 10 E' 081 43 RCL 082 27 27 083 42 STO 084 25 25 085 76 Lbl 086 34 √x 087 73 RCL Ind 088 24 24 089 32 x<>t 090 73 RCL Ind 091 25 25 092 71 SBR 093 11 A 094 43 RCL 095 25 25 096 42 STO 097 24 24 098 61 GTO 099 33 x² 100 76 Lbl 101 10 E' 102 43 RCL 103 26 26 104 42 STO 105 25 25 106 61 GTO 107 34 √x 108 76 Lbl # main 109 15 E 110 42 STO 111 29 29 112 42 STO 113 28 28 114 76 Lbl # 1st heapify 115 13 C 116 22 INV 117 86 St flg 118 01 1 119 43 RCL 120 28 28 121 42 STO 122 00 00 123 01 1 124 22 INV 125 44 SUM 126 00 00 127 76 Lbl 128 18 C' 129 53 ( 130 43 RCL 131 00 00 132 85 + 133 01 1 134 54 ) 135 42 STO 136 25 25 137 53 ( 138 24 CE 139 55 ÷ 140 02 2 141 54 ) 142 42 STO 143 24 24 144 73 RCL Ind 145 24 24 146 32 x<>t 147 73 RCL Ind 148 25 25 149 71 SBR 150 11 A 151 97 Dsz 152 00 0 153 18 C' 154 87 If flg 155 01 1 156 13 C 157 71 SBR 158 32 x<>t 159 76 Lbl # heapify loop 160 35 1/x 161 01 1 162 42 STO 163 24 24 164 71 SBR 165 33 x² 166 71 SBR 167 32 x<>t 168 02 2 169 32 x<>t 170 43 RCL 171 28 28 172 77 x≥t? 173 35 1/x 174 92 RTN 175 76 Lbl # swap + reduce length 176 32 x<>t 177 01 1 178 42 STO 179 24 24 180 43 RCL 181 28 28 182 42 STO 183 25 25 184 71 SBR 185 16 A' 186 01 1 187 22 INV 188 44 SUM 189 28 28 190 92 RTN R00 # pointer R01-23 # Listenelemente R29 # Länge gesamte Liste R28 # Länge aktuelle Liste R27 # Index right leaf R26 # Index left leaf R25 # Index swap leaf R24 # Index top leaf
Die Rechenzeit ist der Mittelwert aus drei Zeitmessungen mit jeweils unterschiedlichen zufälligen Zahlen.
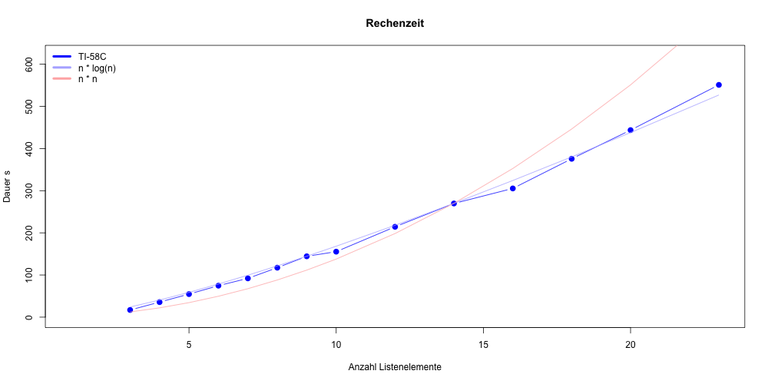
Der Code implementiert den Heap Sort Algorithmus, der in der Laufzeit eine Komplexität von O(n log n) zeigt. Die vorherige Implementation verhielt sich entsprechend O(n*n), war kein Heap-Sort.
Computermuseum

Viele alte lauffähige Computer mit abenteuerlichen Technologien.
Das Bilderalbum. Der angemessene Soundtrack: Kraftwerk It's more fun to compute
technikum29 in Kelkheim. technikum29.de/de/
Depth of field rendering improvement in Blender
This additional code adds realism to the render results of the blender cycles engine. It is possible to simulate some of the optical aberrations occurring when creating a picture with a real camera and camera lens.
The spherical aberration in a real lens is contributing mostly to the appereance of out-of-focus areas in an image. Rays of light entering the lens close to the center (para-axial principal rays) converge in a different focal point than rays entering in the outer areas of a lens (marginal rays). This addition to the code in kernel_camera.h creates this behaviour, it is still a technical test.
Code for altering the direction of a sample ray depending on distance to center of entrance pupil. The focal plane will be different for edge rays than for center rays:
...
float3 P = make_float3(0.0f, 0.0f, 0.0f);
float3 D = Pcamera;
/* modify ray for depth of field */
float aperturesize = kernel_data.cam.aperturesize;
if(aperturesize > 0.0f) {
/* sample point on aperture */
float2 l_uv = camera_sample_aperture(&kernel_data.cam, lens_u, lens_v);
float2 lensuv = l_uv * aperturesize;
/* compute point on plane of focus */
float ft = kernel_data.cam.focaldistance/D.z;
/* distance from center */
+ float dis = sqrt(pow(l_uv.x,2.0) + pow(l_uv.y,2.0));
+ float3 Pfocus = make_float3(D.x, D.y, (D.z * (1.0+(1.0-dis)*0.1) )) * ft;
- // float3 Pfocus = D*ft;
/* update ray for effect of lens */
P = make_float3(lensuv.x, lensuv.y, 0.0f);
D = normalize(Pfocus - P);
}
...
Scene without field of depth

Scene with field of depth, as implemented in blender 2.8

Scene with field of depth and spherical aberration. The Coma effect is also visible in asymmetrical distortion of out-of-focus areas in the image.

The next steps will be to implement some parameters for the other non-chromatic aberrations:
- Spherical aberration
- Coma
- Astigmatism
- Field curvature
- Distortion
Some of the aberrations are depending on each other in some cases. This has to be taken into account. The artist should be able to adjust the parameters idependently.
The additional render time neccessary to achieve a similar image quality might be in a 2-digit percentage range. Some tests have to be done.
Also the displaying, manipulating and storing of parameters should follow the established GUI experience in blender.
Chromatical aberrations will require more changes to the render engine, a native approach will triple the render times at least. More research on algorithms is neccessary.
This approach tries to implement a solution close to the physical / optical realities. It is not a fast software hack. The tradeoff in longer render times might be not acceptable for some artists, desirable for ohters.
Reduzierte Listen

Das Josephus Problem de.wikipedia.org/wiki/Josephus-Problem beschreibt eine Vorschrift für Streichlisten. In einer zyklischen Liste wird umlaufend jedes zweite Element entfernt. Abhängig von der Größe der Liste liefert die Funktion das letzte Element. Der Code für den HP-16C Taschenrechner: :
001 43.22. A Lbl A 002 44 0 STO 0 003 2 2 004 44 1 STO 1 005 43.22. 1 Lbl 1 006 45 0 RCL 0 007 45 1 RCL 1 008 10 ./. 009 43 40 x=0 010 22 2 GTO 2 011 45 1 RCL1 012 2 2 013 20 x 014 44 1 STO 1 015 22 1 GTO 1 016 43.22. 2 Lbl 2 017 45 1 RCL 1 018 2 2 019 10 ./. 020 44 1 STO 1 021 45 0 RCL 0 022 34 x<>y 023 42 9 RMD 024 2 2 025 20 x 026 1 1 027 40 + 028 43 21 RTN
Kamera-Animation in Google Earth
Im Google Earth Browser lassen sich Kameraanimationen aufnehmen, speichern, importieren und als Bildfolge exportieren.
Von vielen Großstädten sind nicht nur einzelne Gebäude als 3D Modelle integriert, sondern das komplette Gelände mit Gebäuden, Bäumen, etc. ist dreidimensional verfügbar. Leider bietet die Animationssteuerung nur wenige Einstellmöglichkeiten, die Qualität der erzeugten Kamerafahrten ist bestenfalls ausreichend.
Mit Hilfe der Dokumente von Google kann man Code erzeugen, der selbst berechnete Animationen in eine syntaktisch korrekte .kml-Datei exportiert.
Die Animationssoftware im Entwicklungsstadium nimmt einzelne aus Google exportierte Kamerapositionen entgegen, berechnet Animationen in hoher zeitlicher Auflösung und erzeugt eine Animation mit Positionsdaten, die in Google als "Tour" importiert werden kann.
Der Beispielfilm basiert auf sechs Positionskeyframes für die Kamera. Die drei Animationen unterscheiden sich nur durch verschieden lange Fenster, um Parameter mit einem gleitenden Durchschnitt zu glätten.
- Fenstergröße 0. Die einzelnen Parameter werden linear überblendet.
- Fenstergröße 6 Sekunden.
- Fenstergröße 22 Sekunden. Der resultierende Bewegungsablauf wird sichtbarer verändert, ist aber deutlich organischer.
Die "Tour" kann in Google Earth importiert, und dort abgespielt werden. ptour06-0300.kml. In dieser Datei sind Keyframes alle 1/50 Sekunde angelegt, entsprechend dem Fernsehstandard.
Die 3n+1 Vermutung

Ein einfach zu beschreibendes Problem ist die 3n+1 Vermutung. de.wikipedia.org/wiki/Collatz-Problem
In der Berechnungsvorschrift ist vorgesehen:
- Anfangswert ist eine natürlichen Zahl n > 0
- Ist n gerade, ist das nächste n = n / 2
- Ist n ungerade, ist das nächste n = 3 n + 1
- Wiederholung Schritt zwei und drei.
Die Folge von Zahlen erreicht irgendwann den Wert 1. Danach ergibt sich eine zyklische Folge 1, 4, 2. Die 3n-1-Vermutung besagt, dass keine Zahl n als Startwert existiert, die nicht nach einer beliebig langen Folge den Wert 1 erreicht.
Die Berechnung der Zahlenfolgen im HP-16C ist mit diesem Programm möglich: :
001 43.22. A Lbl A 002 36 Enter 003 1 1 004 44 8 STO 8 005 33 R↓ 006 43.22. 1 Lbl 1 007 44 9 STO 9 008 1 1 009 43 49 x=y 010 22 4 GTO 4 011 45 9 RCL 9 012 2 2 013 42 9 RMD 014 43 40 x=0 015 22 2 GTO 2 016 45 9 RCL 9 017 3 3 018 20 x 019 1 1 020 40 + 021 22 3 GTO 3 022 43.22. 2 Lbl 2 023 45 9 RCL 9 024 2 2 025 10 ÷ 026 43.22. 3 Lbl 3 027 43 34 PSE 028 45 8 RCL 8 029 1 1 030 40 + 031 44 8 STO 8 032 33 R↓ 033 22 1 GTO 1 034 43.22. 4 Lbl 4 035 45 8 RCL 8 036 43 21 RTN
Der Test auf gerade oder ungerade Zahlen wird im Integer-Modus mit der Funktion RMD (Remainder) umgesetzt. Diese Funktion gibt den Restwert bei einer Integer-Division zurück. Die Division einer Zahl durch zwei ergibt nur bei geraden Zahlen einen Restwert von Null.

