Inharmonische Saitenspektren

In Inharmonic strings and the hyperpiano wird beschrieben, wie mit verschieden starken Segmenten auf einer schwingenden Saite gezielt ein inharmonisches Klangspektrum erzeugt werden kann. Dies bedeutet, dass die Frequenzen der Teiltöne nicht zwangsläufig ganzzahlige Vielfache der Grundfrequenz sein müssen. Die numerische Lösung erfordert Matrixoperationen und ein Näherungsverfahren zur Nullstellensuche. Diese Herausforderung ist mit programmierbaren Taschenrechnern lösbar.

Im HP-42S werden die verschieden starken Saitensegmente jeweils durch eine 2x2 Matrix repräsentiert, das Produkt der Matrizen gibt in einer Zelle als Nullstelle die Frequenzen der Teiltöne. Der eingebaute Solver erledigt die Nullstellensuche mit entsprechend eingegrenztem Suchbereich zuverlässig.

 01     LBL "INHX"              # Main-Loop für den Solver
 02     MVAR "W"
 03     RCL "Vµ1"
 04     STO "µ"
 05     RCL "VL1"
 06     STO "L"
 07     XEQ "MTRX"
 08     STO "MZ"
 09     RCL "Vµ2"
 10     STO "µ"
 11     RCL "VL2"
 12     STO "L"
 13     XEQ "MTRX"
 14     STOx "MZ"
 15     INDEX "MZ"
 16     1
 17     ENTER
 18     2
 19     STOIJ
 20     RCLEL
 21     RTN
 22     .END.

 01     LBL "MTRX"              # Berechnung der Matrix für ein Saitensegment
 02     2
 03     ENTER
 04     2
 05     NEWMAT
 06     STO "MT"
 07     INDEX "MT"
 08     RCL "µ"
 09     RCL "T"
 10     /
 11     SQRT
 12     RCL "W"
 13     x
 14     STO "K"
 15     RCL "L"
 16     x
 17     STO "KL"
 18     COS
 19     STOEL
 20     1
 21     ENTER
 22     2
 23     STOIJ
 24     RCL "KL"
 25     SIN
 26     RCL "K"
 27     /
 28     +-
 29     STOEL
 30     2
 31     ENTER
 32     1
 33     STOIJ
 34     RCL "KL"
 35     SIN
 36     RCL "K"
 37     x
 38     STOEL
 39     2
 40     ENTER
 41     2
 42     STOIJ
 43     RCL "KL"
 44     COS
 45     STOEL
 46     RCL "MT"
 47     RTN
 48     .END.

 µ      Dichte des Segments
 Vµ1    Dichte 1
 Vµ2    Dichte 2
 T      Saitenspannung
 L      Länge des Segments
 VL1    Länge 1
 VL2    Länge 2

Mit unterschiedlichen Längen der dichten und leichten Saitensegmente ergibt sich eine Verschiebung der Frequenzen der Teiltöne, die Saite klingt Inharmonisch, "metallischer".

Die Berechnung basiert auf zwei Saitensegmenten. Weitere Versuche müssen zeigen, inwieweit mehr Segmente die Verschiebung der Teiltöne beeinflussen. Das nächste Ziel ist, für ein beliebig vorgegebenes Spektrum (für Konsonanzoptimierung in einer beliebigen Skala) mittels eines Gradientenabstiegverfahrens die Position und Länge von Saitensegmenten zu berechnen / optimieren.

Aus Performance-Gründen wird die Umsetzung in einer modernen PC-Umgebung stattfinden. ;-)

Faktoren für Frequenzen der Teiltöne

Der Dichteunterschied für verschiedene Saitensegmente und die Längen der Teilstücke scheinen offensichtliche Faktoren für die Verteilung der Frequenzen der Teiltöne zu sein. [Die Saitenspannung ändert zwar die Tonhöhe, aber nicht die Frequenzverteilung der Teiltöne] (Dies ist noch zu klären).

Bei drei verwendeten Segmenten zeigt sich, dass die Position des mittleren, schweren Teilstücks Einfluss auf die Teiltonfrequenzen hat. (Länge Mittelteil (0,2) und Gesamtlänge (1,0) bleiben konstant)

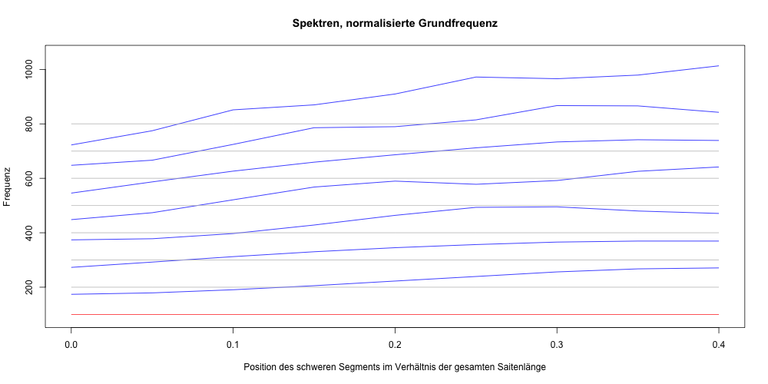
Je weiter ein schweres Mittelstück zur Saitenmitte wandert, umso weiter wandern die Teiltöne unterschiedlich auseinander. (x ≈ L1)

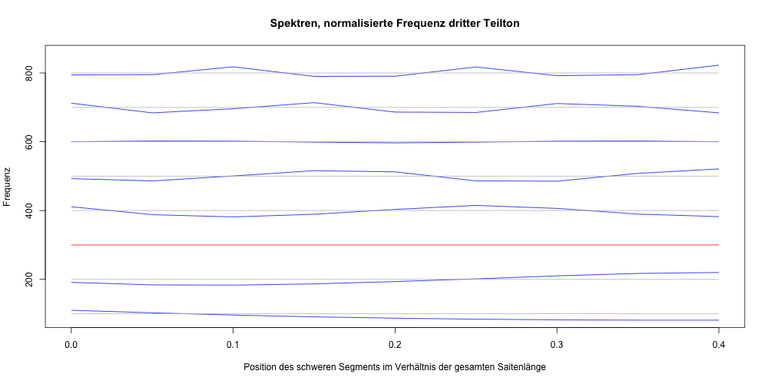
Die Frequenzen des dritten Teiltons gleich gestimmt:

Anzahl der Segmente

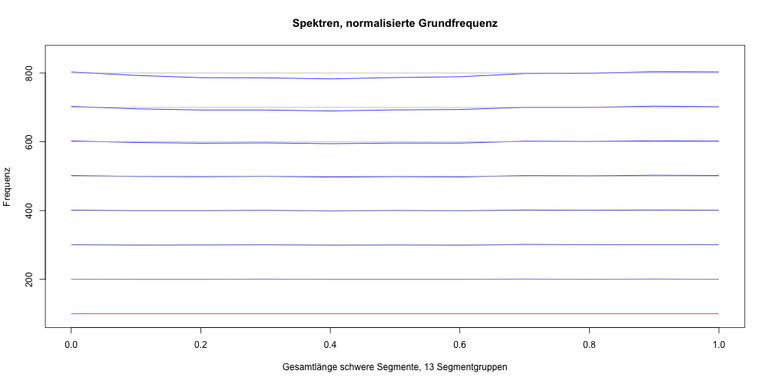
Ein gleichbleibendes Verhältnis der Gesamtlänge von schweren zu leichten Saitensegmenten erzeugt bei unterschiedlicher Verteilung verschiedene Spektren. Eine Segmentgruppe besteht hier aus zwei gleich langen, verschieden schweren Teilstücken. Die Anzahl der Segmentgruppen wird variiert.

Bei gleichbleibender Anzahl der Segmentgruppen mit verändertem Verhältnis von schweren und leichten Teilstücken zeigt sich keine nennenswerte Änderung in der Verteilung der Teiltonfrequenzen. Vorausgesetzt es werden Teiltöne betrachtet, deren Wellenlänge größer als die Länge einer Gruppe schweres / leichtes Saitensegment ist. Hier 13 Segmentgruppen, Darstellung bis zum 8. Teilton.

Der Soundtrack zum Projekt. ;-)